
Similarly the 2 nd Quartile (identically equal to the 50 th Percentile) can be calculated by entering =Quartile(B2:B19, 2). Therefore 50% of the data lies above 54.5 and 50% below. NB: sorting is not essential for percentiles but it helps us see how Percentile and Quartile work in practice.įor example to calculate the 50 th percentile key in, =Percentile(B2:B19, 0.50) into cell D10 (or any cell) and press enter. Sort the data as shown – from smallest to largest numbers. 1 st quartile = 25 th percentile, 2 nd quartile = 50 th percentile (also the median) and 3 rd quartile = 75 th percentile. Quartiles are simply specific Percentiles, e.g. Percentiles indicate the percentage of values that lie below the percentile value. This implies that students were equally as likely to score above the mean as below it.įinally, there are two other measures that provide information about how the data is spread – they are Percentiles and Quartiles. The spread of values is evenly distributed around the mean and the median. The mean and the median are relatively close in value (mean = 53 and median = 54.5) indicating that the distribution of results are not significantly skewed to one end. These two values could be outlier values thereby give a false indication of the spread of the data. However the Range is limited by the fact that it only uses 2 values.
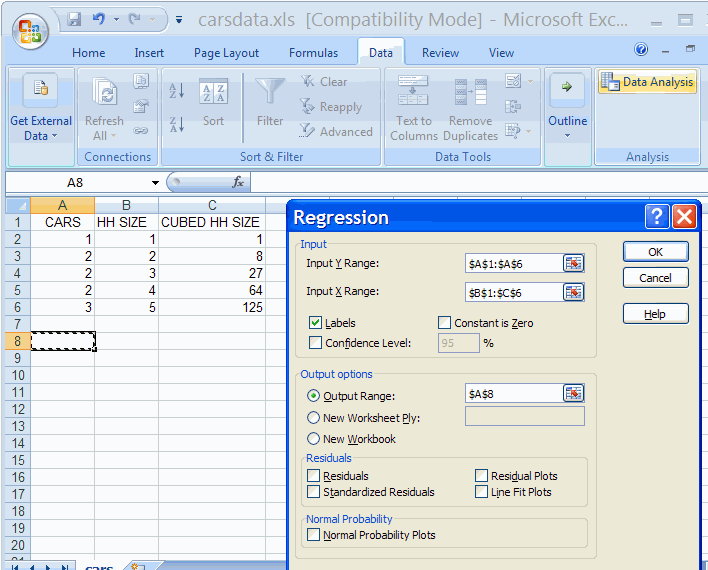

This indicates how dispersed the data is, considering the test was scored out of 100. As can be seen from the data analysis table, the spread for history scores is from 7 to 100 – equating to a range of 93 marks.


 0 kommentar(er)
0 kommentar(er)
